Abstract: Configuration Space, short as C-Space, is a map for a roboticist finding some collision-free paths with a robot. A lot people don't get this idea truly understand and become confused in the next learning step. I'm going to contribute all my knowledge on this, trying to keep the article short and hit the key points.

Goal

Don't forget at any point, our goal is find a trajectory for a robot traveling from an initial posture to a goal posture.

• Posture: the robot's position + orientation.

• Trajectory: a sequence of trajectory elements.

• Element: a posture + a time frame.

In all, we want find a time sequence of elements. Each element includes some parameters of the robot and if we somehow make the robot to execute this sequence, it will finally arrive at our goal !

How to make it happen?

If we through all these parameters in the world of computer(science), it is the C-Space. Once we have a init and a goal, it become an equation: Init (x) C-Space = Goal. All we need to do is sit down and drink a coffee, wait for the computer to find the answer. Fantastic !

Recall: A C-Space is not only the set of the robot's joints configurations but also the all possible postures where it could be in the workspace.

The Maze of a C-Space

Let's start from a Human level example. Suppose we have this simple 2D maze and we want to start with the green point, end at the red point.

There are a lot algorithms can help us finding the path (remember a path is just a simple line of walking without hitting any obstacles). The easiest one would be line up these two points and check collision on the router, if hit, then follow the obstacle, either right or left and always going towards the red point if possible.

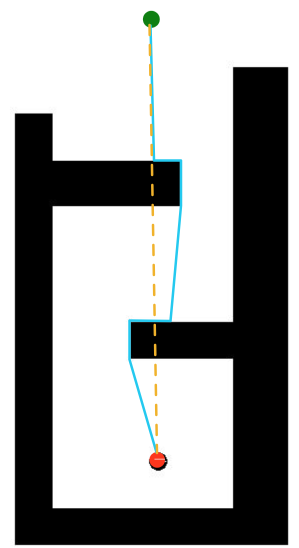
The orange line is our intuitive direction and the sky-blue line is our true path.

Recall that this is our final goal! Several parts engaged in this problem are:

1. Will the robot always be a point?
2. How to make the maze can be read by a computer?
3. Is there a smarter algorithm that finds the path?
4. When you say check collision, as a human I understand but a computer, how?
5. My name is Peng and this is my notes.

For Q1, the general idea is reduce the robot size and enlarge the obstacle's. Like this:

In motion planning, the key concept of configuration is:

A complete specification of the position of every point in the system. [^n]

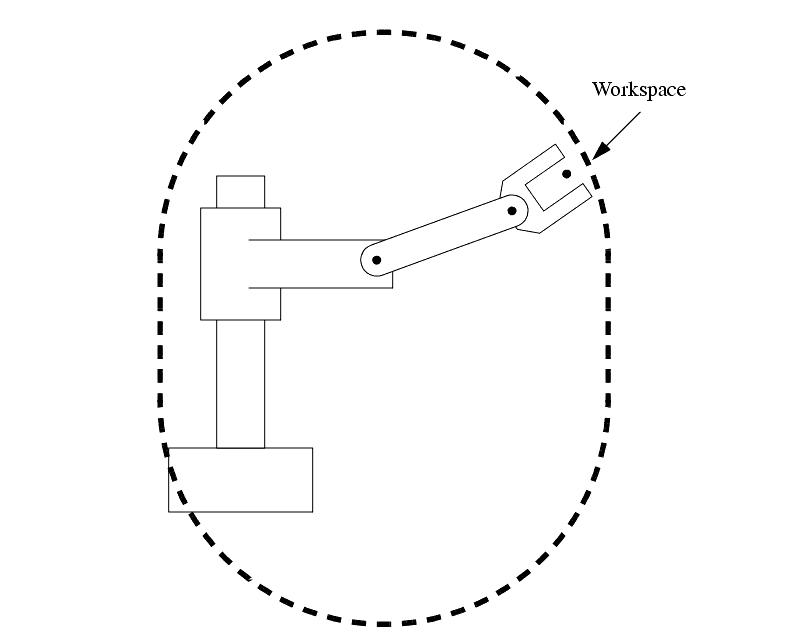
Now let's be sure you know some item about the "space". A workspace (sometimes known as reachable space) is all places that the end effector (gripper) can reach. [^n]

When you "add" the workspace to the obstacles you are going to get the remaining part as free-space and the whole part as the C-space. In this example, the as robot's workspace become larger you can see its C-space get changed.

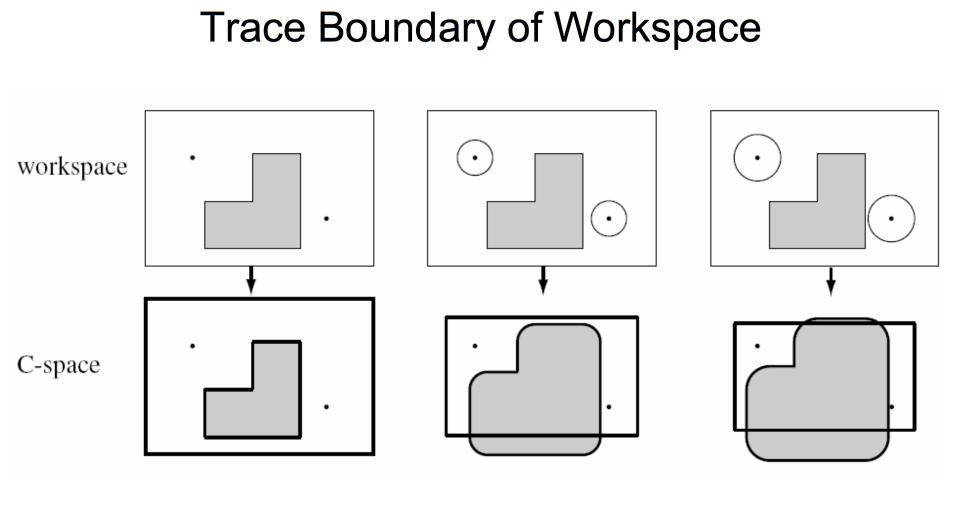
One more example on how to do this.

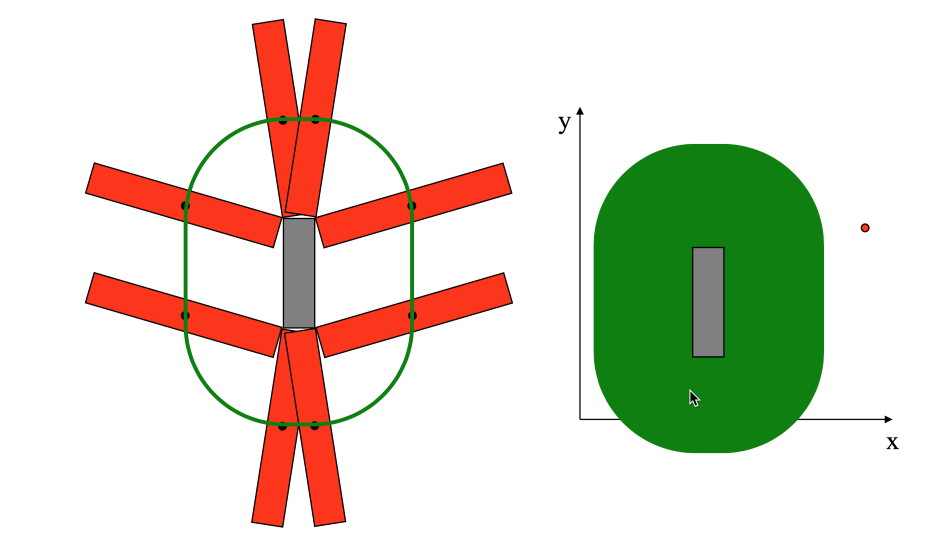
2D Shape with Rotation

Now life becomes harder. We finish talking about a 2D shape only have transforms and we are going to talk about a 2D shape with transforms and one single rotation.

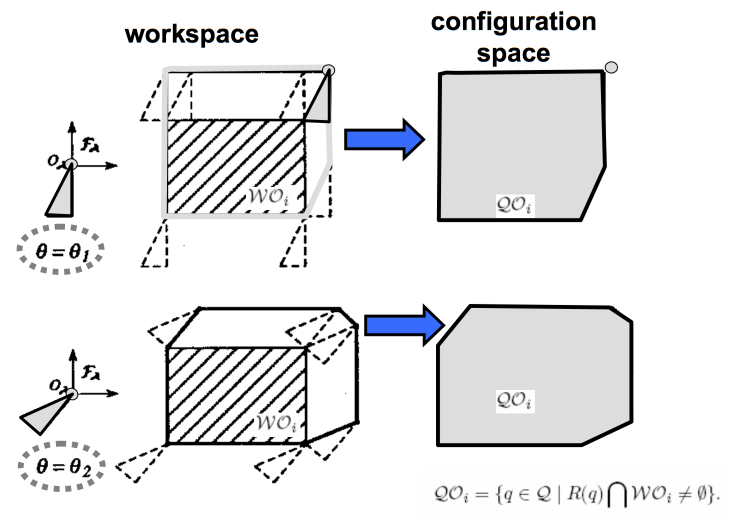
We layer the theta rotation up as the Z-axis in Cartesian space. You will see a strange object. This space is in SE(2), we will talk about this later in anther note.

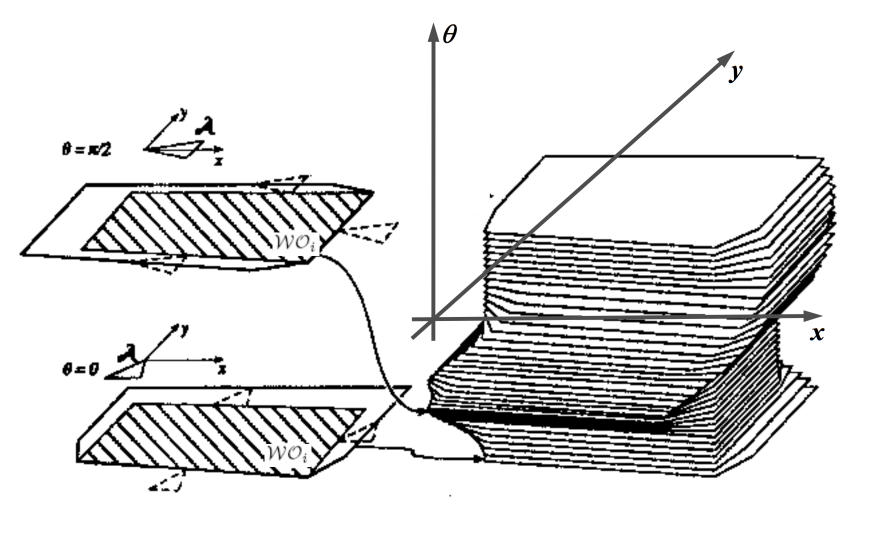
Result

By having the knowledge above, we now have a wonderful map that tells us how to solve reach the goal of the labyrinth, cheers! Let's see this result of a successful 2D rigid body planning.

Job Done !
But wait... don't we miss some part of the problem?

Yes! If you are clever enough, we skip the part "how to check collisions" because this is something related to topology. Which is super hard. However, don't worry. I'll buy some coffee and scarify myself to eat about this in next note.

[1]: Some Pictures and Quotes are referenced from Howie's Lecture slides.

[2]: Robot Arm Tutorial - How to Build a Robot Tutorials