Abstract: A Star Algorithm has been widely used in motion planning problems. This article will start from a real project to help you understand the A Star programing idea. It is nice because we will use PR2 in OpenRave as an example.

Python Tips:

• Use deepcopy() when you append an item in for loop
• Set attributes before copy if you are using deepcopy()
• If you spend > 5 lines to implement a function, make it a function and call it.

Preparation

If you never touched A* before, I suggest you go to the reference section and try out those two guidelines. This article will be more programming focused.

The problem set finds a trajectory for the PR2 robot from the Starting posture(Left) to the Ending posture(Right).
Let's first see the result of a general idea of the problem.

(Black points are collision-free trajectory; blue points are collision-free neighbors; red points are the neighbors in the collision. Notice that the drawings may be layered)

A* is under the big title of discrete motion planning. When you are talking about this, it is almost saying that we are going to slice the C-Space into tons of grids(To understand C-Space, view this post).

Now let's talk about what we need. Obviously, a class that represents the neighbors in the grid(which also called map) should be created. Be careful with the precision of H&G values, if we define them as self.H = 0, then there will be a type cast whe you assign values to them. We are just so sure about the return value won't be an integer.

class Node:
    def __init__(self,point3d):
        self.point = point3d
        self.parent = None
        self.H = 0.
        self.G = 0.

One step further, if we are in a C-Space, each of the points in it should have n axises, for example, a 3D point will be (x,y,z), so a 10D point will be (x,y,z,...). Therefore, a class represents the point position should also be created.

class Point3D:
    def __init__(self,array3d):
        self.x = Float(str(array3d[0]),DIGITS)
        self.y = Float(str(array3d[1]),DIGITS)
        self.z = Float(str(array3d[2]),DIGITS+2)
    def __repr__(self):
        return "(%s, %s, %s)"%(self.x,self.y,self.z)

Need to notice: the default float value of python is very "float" style, its digits will blow you away if not handling them properly. Float is a nice looking symbolic expression class, to use this we need to import sympy at the beginning.

from sympy import *
from copy import deepcopy

The A Star Algorithm

Now let's start to write the A*.

def AStar(start,goal,env,robot,handler,refine = False):
    startNode = Node(Point3D(start))
    goalNode = Node(Point3D(goal))

    openSet = set()
    closedSet = set()

These two sets will be filled with neighbor nodes, let's just call them neighbors. Notice that use set() instead of a list[] will improve your running speed. This is because the openSet serves as a priority queue or a min-heap or whatever gives the min F value on each loop. So there is NO reason for an indexable neighbor container.

Then, we do a little thing to handle our inputs, which are Nodlizing the starting point and ending point.

    startNode = Node(Point3D(start))
    goalNode = Node(Point3D(goal))

    startNode.G = 0.
    startNode.H = manhattan(startNode.point,goalNode.point)

    currentNode = startNode
    openSet.add(currentNode)

I've made a start and goal become two instances of the Node class which is special neighbors. After calculating H&G values, I put the startNode in the openSet then we can let the A* rolling from here!

Wait a minute...did I just miss something? H&G values? How? Ok, so we gonna add a function to the Node class, make it callable to return our H values that indicates the move cost. Please don't worry about the refine stuff.

This cost function will use Manhattan method to check the number of variants on each direction. For example, if the current node is at (4,5,6) and checks with a neighbor (4,6,7), so the number of variants is '2' and should return the cost. In a 3D 8-Connect case, if all move cost is positive, there should be only three types of cost. Notice that this snippet is bugged because I should relate the checking value with step sizes, for instance, 1.0001 * StepSize instead of making it a constant value of 1.0001.

   def move_cost(self,other,refine=False):
        # mask out change in 1/2/3 directions against the center of the connections
        grids = manhattan(self.point, other.point)

        if not refine:
            if grids < Float('1.0001'):
                return Float('10',1)
            elif grids < Float('2.0001'):
                return Float('14',1)
            else:
                return Float('17',1)

On the other hand, the heuristic functions here are truly nothing to say just make an eye on that how to make square root in python efficiently.

def manhattan(point1,point2):
    return abs(point1.x-point2.x) + abs(point1.y-point2.y) + abs(point1.z-point2.z)

def euclidean(point1,point2):
    return ((point1.x-point2.x)**2 + (point1.y-point2.y)**2 + (point1.z-point2.z)**2)**0.5

Ok, now let's get back to the business. While there are still some neighbors haven't been searched, take the one has minimum F value for this turn:

    while len(openSet) > 0:
        currentNode = min(openSet,key=lambda o:o.H + o.G)

I know this lambda thing looks fancy but it is nothing other than a shorthand function. The lambda o:o.H + o.G picks an object in the openSet and returns the sum of H&G value. In case you want to learn more about lambda, read this article.

After picking up the node, the next step is to make sure that this guy is not the goal. Otherwise, we finish the search and return the path. It looks cool when you use path[::-1] to reverse a list, which equals to path.reverse().

            # if it's the goal, we retrace the path from parents and return it
            if check_points(currentNode.point.value(),goalNode.point.value()): 

                path = []
                while currentNode.parent:
                    path.append(deepcopy(currentNode))
                    currentNode = currentNode.parent
                # the start node does not have a parent
                path.append(currentNode)
                return path[::-1]

Notice that the nodes are objects, it is NOT making any sense to compare two objects but their member's values. In order to do this, another function has to be done:

def check_points(point1,point2):
    if (abs(point1[0]-point2[0])<0.01)&(abs(point1[1]-point2[1])<0.01)&(abs(point1[2]-point2[2])<0.001):
        # print point1,point2, 'True'
        return True
    else:
        # print point1,point2, 'False'
        return False

Recall the way to compare two float points is to compare their difference with 0.000001, to compare their difference with 0.000001, to compare their difference with 0.000001. Important things yield three times.

One last thing before using A* to search is that how to find neighbors for the currentNode? It is very simple base one the StepSize you are giving. I'm listing a 8-Connect neighbor generator here and for the 4-Connect one you can just write all the neighbors down.

def neighbors_8C(currentNode,STEPS,env,robot,handler,pointSize):
    # Symboalize the float numbers so we can get pretty results
    xi,yi,zi,XSTEP,YSTEP,ZSTEP = stepsHandler(currentNode,STEPS)
    # 8-connect neighbor generator
    neighborNodes = set()
    for x in xrange (-1,2):
        for y in xrange (-1,2):
            for z in xrange (-1,2):
                neighborNode = Node(Point3D([xi+XSTEP*(x),yi+YSTEP*(y),zi+ZSTEP*(z)]))
                if check_collision(neighborNode,env,robot) or (x,y,z) == (0,0,0):
                    # take out 'Center Point' and colliding points
                    drawingDispatcher(handler, env, neighborNode, COLORS["red"],pointSize)
                    continue
                else:
                    drawingDispatcher(handler, env, neighborNode, COLORS["blue"],pointSize)
                    neighborNodes.add(neighborNode)

    return neighborNodes

Now we have the main A* search party here. First thing is to move the current node into closedSet, if you forget to do this, your code will never finish until you control + C.

The idea here is to explore all neighbors of current node, skip those neighbors that once was a currentNode, update those neighbors who have a better path (considering walking from beginning).

        openSet.remove(currentNode)
        closedSet.add(currentNode)

        for neighborNode in neighbors_8C(currentNode,STEPS,env,robot,handler,pointSize):
            if nodeIsInClosedSet(neighborNode,closedSet):
                continue
            tentative_g = currentNode.G + currentNode.move_cost(neighborNode,refine)

Notice that for the very first run because we remove the startNode from openSet so there is actually no neighbors for the empty checking. We have to handle this special case.

            # this node is not from closeset
            if len(openSet) == 0:
                neighborNode.G = tentative_g
                neighborNode.parent = currentNode
                neighborNode.H = manhattan(neighborNode.point,goalNode.point)
                openSet.add(deepcopy(neighborNode))

Below is the regular update follows the sudo code from Wiki.

            else:
                if not nodeIsInOpenSet(neighborNode,openSet):
                    # New H score evaluation 
                    neighborNode.H = euclidean(neighborNode.point,goalNode.point)
                    neighborNode.parent = currentNode
                    if tentative_g < neighborNode.G:
                        neighborNode.G = tentative_g
                    openSet.add(deepcopy(neighborNode))

Dont forget to raise an Error when no path are found and basically no path exists.

    raise ValueError('No Solution Found.')

All Done!

About the Refine Step

Here is what it is used for: Searching tons of neighbors aren't easy stuff. Although in this case, it is only a 3D problem and with not much rotation needed, we still want it runs fast!

So A* searching begins big step sizes. When the currentNode is near goalNode, we start to run small step sizes to have a thorough search to ensure the accuracy of our solution.

This is done by calling A* recursively. This is an extra part of the article in case you want to know how:

    while len(openSet) > 0:
        currentNode = min(openSet,key=lambda o:o.H + o.G)
        if not refine:
            # if it's the goal, we retrace the path from parents and return it
            if check_points2(currentNode.point.value(),goalNode.point.value()): 

                path = []
                path2 = AStar(currentNode.point.value(),goal,env,robot,handler,True)

                while currentNode.parent:
                    path.append(deepcopy(currentNode))
                    currentNode = currentNode.parent
                # the start node does not have a parent
                path.append(currentNode)
                path.reverse()
                # our final path
                return path+path2
        else:
                ...

And here is the collision checking method:

def check_collision(node,env,robot):
    # set the robot to the location
    robot.SetActiveDOFValues(node.point.value())
    return env.CheckCollision(robot)

One more Notice: the code snippets are not in order and adjusted to make a clear point of view. Please contact me if you need help other than the source code.

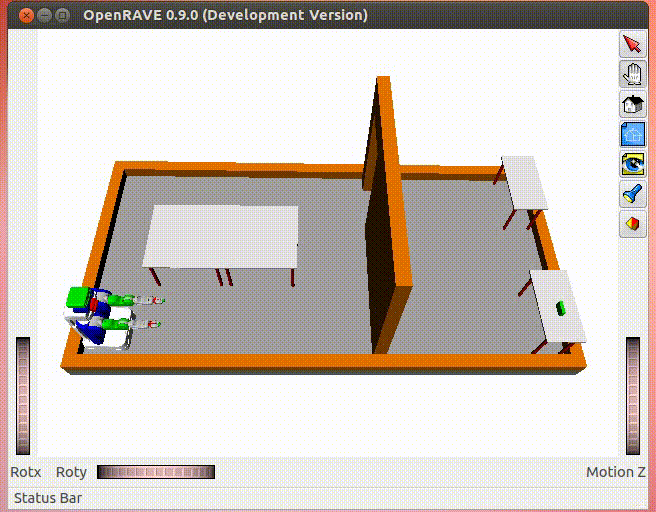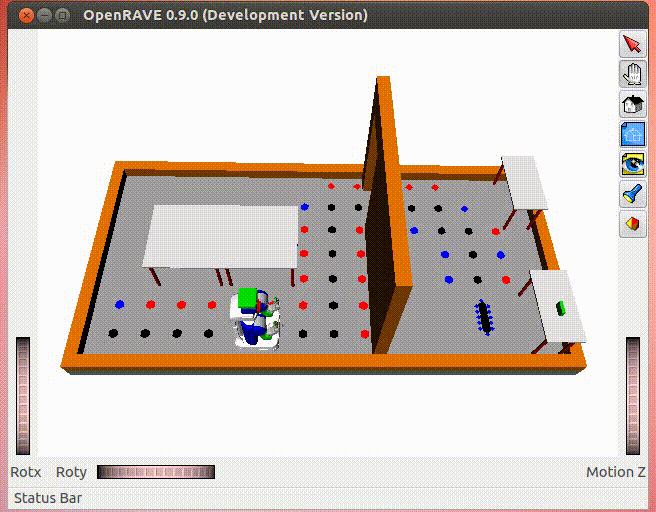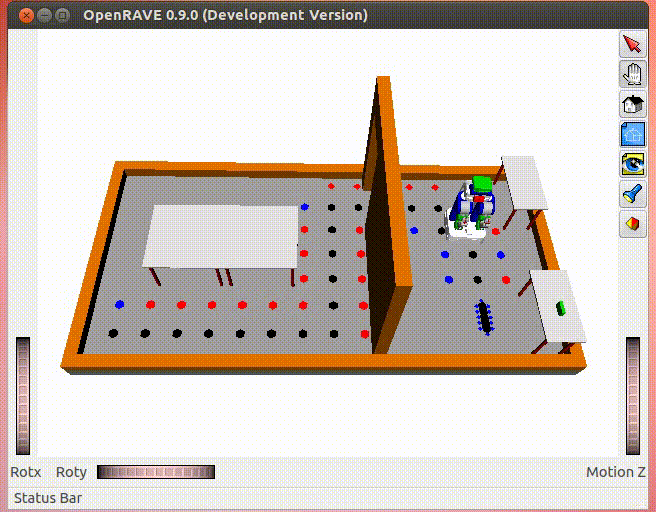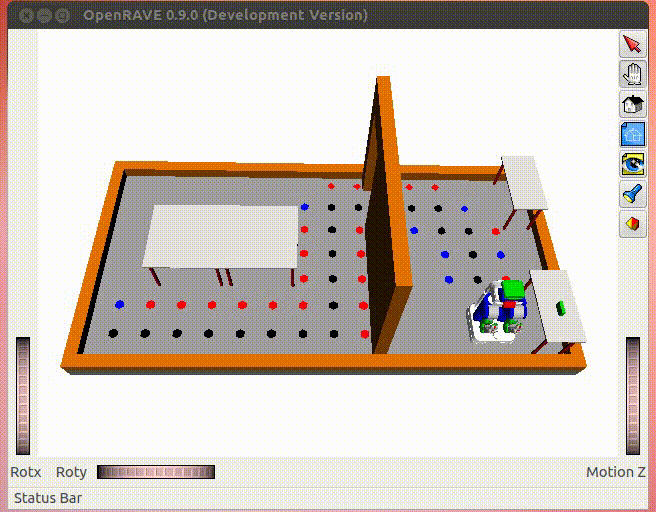
The GIF shows an example of 4-Connect Manhattan A* search that runs very fast in this problem. You will see how to refine method works beautifully at the end.

Well, thank you for reading and hope your life becomes better!

Reference

There are two resources that I recommend you to read first. This one is from Wiki and it is very traditional and let you easy to catch the idea of A Star Algorithm.

This one is from MIT it takes some black magic to guide your program faster with less problem. Aditya provides the link.