Back-propagation in Neural Network, Octave Code
Abstract: This post is targeting those people who have a basic idea of what neural network is but stuck in implement the program due to not being crystal clear about what is happening under the hood. If you are fresh new to Machine Learning, I suggest you bookmark this post and return to it in the future.
Try answering these three questions may help you to decide if the reset of this post will help you:
- What is a, z and big Theta?
- Does a or z include the bias node? How about the big Theta?
- What is small delta and big Delta? Are they in the same order?
If you can't be clear about the questions, please continue reading; otherwise, abort.
What is a Neural Network indeed?
It is no other than something like a logistic regression classifier that helps you to minimize the Theta sets and outputs a result telling your input belongs to which class.
For instance, given a picture of a handwriting "one", the program should output a result says the query belongs to One's class.
As you guys supposed, I will post the core part first.
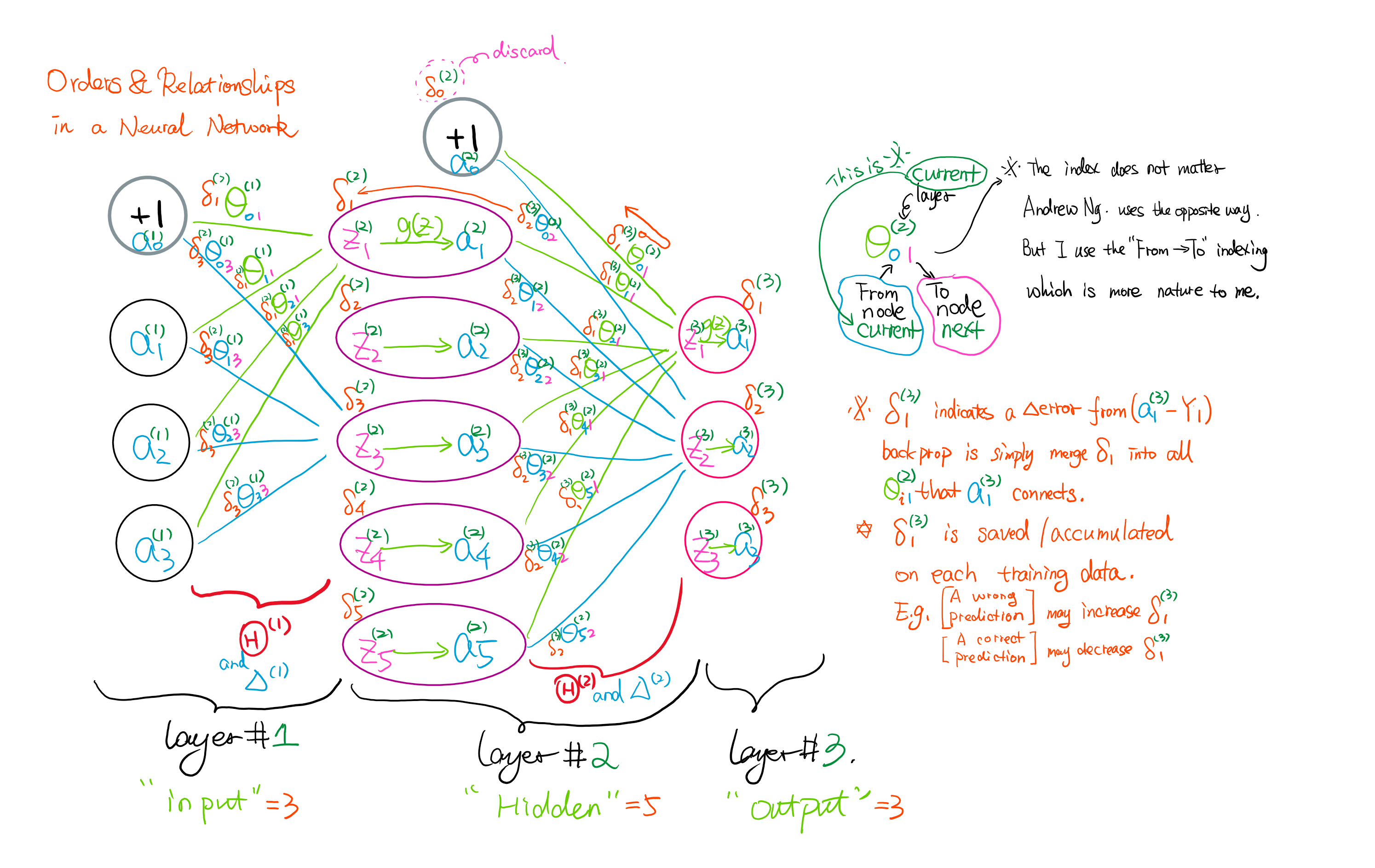
This example shows a simple three layers neural network with input layer node = 3, hidden layer node = 5 and output layer node = 3.
I draw out only two theta relationships in each big Theta group for simpleness.
You should study this Neural Network "Guidelines" picture with the questions below:
- Is there a layer 0?
- Which layer contains a bias unit?
- Is there a node called a0 in each layer?
- What is z? Is it a vector starts at z1?
- What is the size difference between a and z in the same layer?
- The big Theta belongs to the layer on its left or right?
So these questions are for Feedforward procedure and they are easy to get the answer from the drawings. It is also not hard to implement this part.
Back-Propagation
The key to solving this in programming is you have to know where to strip off the bias unit that we used in Feedforward. So what is Back-propagation? It is a way to help you calculate the gradients of big Theta faster. It measures the error effect from the output layer and propagates back the affectedness.
For example, back propagate theta1^(3) from a1^(3) should affect all the node paths that connecting from layer 2 to a1^(3).
Note and this is important: when you propagate from layer 2 to layer 1, you should not include the theta from the bias node!
I wrote down the details of the matrix demissions in calculating the whole network. Check them step by step will be helpful.
Just in case you forget how to do matrix multiplication in a row:
Now Implement It! Please Think carefully if you want to continue!
Some quick steps for you to reference. Pictures snapped from Andrew's class. I also recommend you using their code framework to skip the less important part, which builds up the testing part and make your coding experience no fun if you do it by yourself.
You can download the assignment from here.
function [J grad] = nnCostFunction(nn_params, ...
input_layer_size, ...
hidden_layer_size, ...
num_labels, ...
X, y, lambda)
%NNCOSTFUNCTION Implements the neural network cost function for a two layer
%neural network which performs classification
% [J grad] = NNCOSTFUNCTON(nn_params, hidden_layer_size, num_labels, ...
% X, y, lambda) computes the cost and gradient of the neural network. The
% parameters for the neural network are "unrolled" into the vector
% nn_params and need to be converted back into the weight matrices.
%
% The returned parameter grad should be a "unrolled" vector of the
% partial derivatives of the neural network.
%
% Reshape nn_params back into the parameters Theta1 and Theta2, the weight matrices
% for our 2 layer neural network
Theta1 = reshape(nn_params(1:hidden_layer_size * (input_layer_size + 1)), ...
hidden_layer_size, (input_layer_size + 1));
Theta2 = reshape(nn_params((1 + (hidden_layer_size * (input_layer_size + 1))):end), ...
num_labels, (hidden_layer_size + 1));
% Setup some useful variables
m = size(X, 1);
% You need to return the following variables correctly
J = 0;
Theta1_grad = zeros(size(Theta1));
Theta2_grad = zeros(size(Theta2));
% Modify this to use the vec calculation, which is way faster 10x faster
% 0: use for loop
% 1: use vec ops
use_vectorizing = 0;
% ====================== YOUR CODE HERE ======================
% Instructions: You should complete the code by working through the
% following parts.
%
% Part 1: Feedforward the neural network and return the cost in the
% variable J. After implementing Part 1, you can verify that your
% cost function computation is correct by verifying the cost
% computed in ex4.m
%
if use_vectorizing == 0
for i = 1:m
%The raw neuros counts the bias unit, which means it as a0 -> a25, not count a1
a1 = [1 X(i,:)]'; % insert the bias unit
z2 = Theta1 * a1;
a2 = [1 ; sigmoid(z2)];
z3 = Theta2 * a2;
a3 = sigmoid(z3);
hx = a3;
y_vec = zeros(num_labels,1);
y_vec(y(i)) = 1; % this the compare y to be a binary vector
one_query_cost = (-y_vec' * log(hx) - (1 - y_vec') * log(1 - hx));
J = J + one_query_cost;
% Part 2: Implement the backpropagation algorithm to compute the gradients
% Theta1_grad and Theta2_grad. You should return the partial derivatives of
% the cost function with respect to Theta1 and Theta2 in Theta1_grad and
% Theta2_grad, respectively. After implementing Part 2, you can check
% that your implementation is correct by running checkNNGradients
%
% Note: The vector y passed into the function is a vector of labels
% containing values from 1..K. You need to map this vector into a
% binary vector of 1's and 0's to be used with the neural network
% cost function.
%
% Hint: We recommend implementing backpropagation using a for-loop
% over the training examples if you are implementing it for the
% first time.
%
y_vec = zeros(num_labels,1);
y_vec(y(i)) = 1; % this the compare y to be a binary vector
delta3 = (a3 - y_vec);
delta2 = (Theta2(:,2:end)' * delta3) .* sigmoidGradient(z2);
Theta2_grad = Theta2_grad + delta3 * a2';
Theta1_grad = Theta1_grad + delta2 * a1';
endfor % Missing this 'end' to close the loop cost me more than three hours to debug.
% Part 3: Implement regularization with the cost function and gradients.
%
% Hint: You can implement this around the code for
% backpropagation. That is, you can compute the gradients for
% the regularization separately and then add them to Theta1_grad
% and Theta2_grad from Part 2.
%
% Theta 0 does not involve in the regularlization From Cost Fn
theta2_reg = Theta2; theta2_reg(:,1) = 0;
theta1_reg = Theta1; theta1_reg(:,1) = 0;
% Regularlization of the Averaged cost function
J = J / m + lambda / (2 * m) * (sum( (theta1_reg.^2)(:) ) + sum( (theta2_reg.^2)(:) ) );
Theta2_grad = Theta2_grad / m + lambda / m * theta2_reg;
Theta1_grad = Theta1_grad / m + lambda / m * theta1_reg;
endif
% -------------------------------------------------------------
% =========================================================================
% an alternative solution
if use_vectorizing > 0
% recode y to Y, a good way to learn
I = eye(num_labels);
Y = zeros(m, num_labels);
for i=1:m
Y(i, :)= I(y(i), :);
endfor
% feedforward
a1 = [ones(m, 1) X];
z2 = a1*Theta1';
a2 = [ones(size(z2, 1), 1) sigmoid(z2)];
z3 = a2*Theta2';
a3 = sigmoid(z3);
h = a3;
% calculte penalty
p = sum(sum(Theta1(:, 2:end).^2, 2))+sum(sum(Theta2(:, 2:end).^2, 2));
% calculate J
J = sum(sum((-Y).*log(h) - (1-Y).*log(1-h), 2))/m + lambda*p/(2*m);
% calculate deltas
delta3 = a3.-Y;
delta2 = (delta3*Theta2(:,2:end)).*sigmoidGradient(z2);
% accumulate gradients
Delta1 = (delta2'*a1);
Delta2 = (delta3'*a2);
% calculate regularized gradient
Theta1_reg = Theta1; Theta1_reg(:,1) = 0;
Theta2_reg = Theta2; Theta2_reg(:,1) = 0;
p1 = (lambda/m) * Theta1_reg;
p2 = (lambda/m) * Theta2_reg;
Theta1_grad = Delta1 / m + p1;
Theta2_grad = Delta2 / m + p2;
endif
% Unroll gradients
grad = [Theta1_grad(:) ; Theta2_grad(:)];
end